2022年硕士研究生《数学(三)》模拟卷(一)
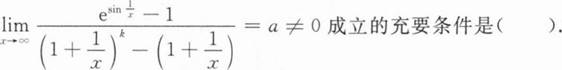
A.k≠1
B.k>1
C.k>0
D.与k无关
A
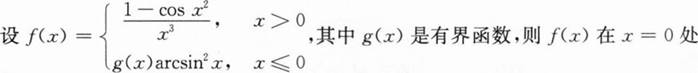
A.极限不存在.
B.极限存在,但不连续.
C.连续,但不可导.
D.可导.
C
A.
B.
C.
D.
C
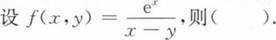
A.
B.
C.
D.
D
A.若m B.若m>n,则方程组AX=b一定有唯一解 C.若r(A)=n,则方程组AX=b一定有唯一解 D.若r(A)=m,则方程组AX=b一定有解
D
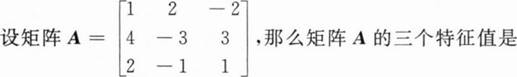
A.1,0,-2.
B.1,1,-3.
C.3,0,-2.
D.2,0,-3.
D
A.f=
B.f=2
C.f=
D.f=2
B
A.相关且相互独立
B.不相互独立但不相关
C.不相关且相互独立
D.相关但不相互独立
B
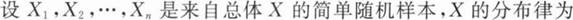
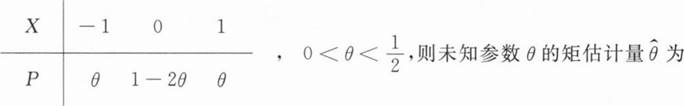
A.
B.
C.
D.
D
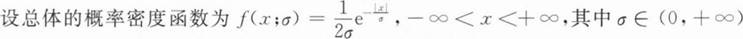
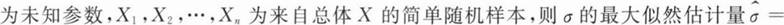
A.
B.
C.0
D.
B
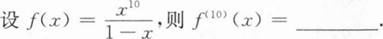
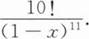
【解析】
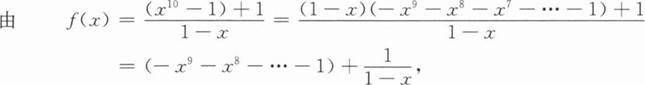


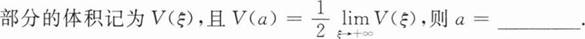
1
【解析】

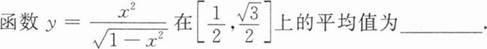
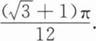
【解析】
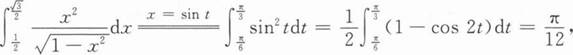

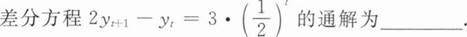
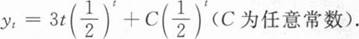
【解析】
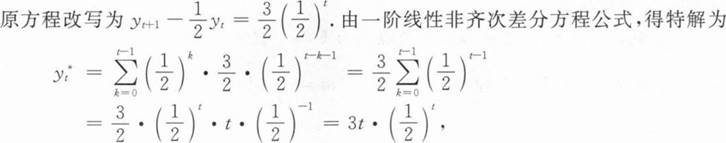
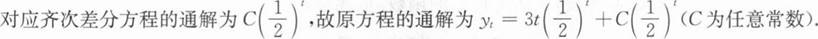

6
【解析】
若按第1行展开,只有-2x乘以其代数余子式会出现x3项,故只要求出这一项即可.
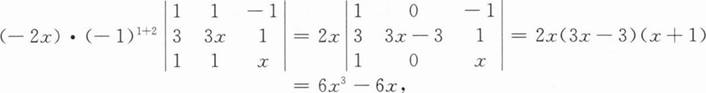
故x3的系数为6.
1
【解析】
D(Y)=4D(X)=36,

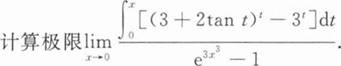
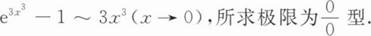

解(Ⅰ)
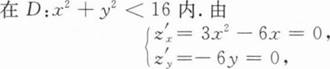
得驻点(0,0),(2,0).
(Ⅱ)在D:x2+y2=16上.
 得(0,±4).(±4,0).
得(0,±4).(±4,0).(Ⅲ)比较大小z(0,0)=0,z(2,0)=-4,z(0,4)=-48,
z(0,-4)=-48,z(4.0)=16,z(-4,0)=-112,
得最大值为z(4,0)=16.
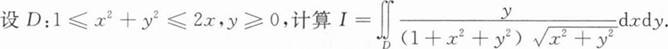
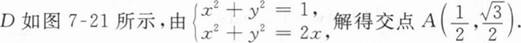
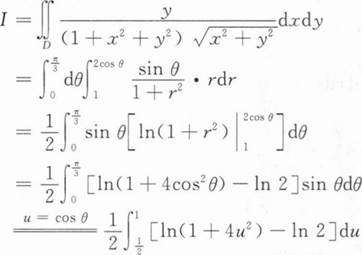
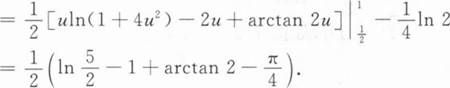
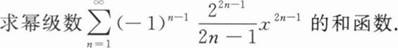
【解】


 α1=(1,1,0)T,α2=(0,2,1)T.
α1=(1,1,0)T,α2=(0,2,1)T.(Ⅰ)求A的特征值与特征向量;
(Ⅱ)求可逆矩阵P,使得P-1AP=Λ.
解(Ⅰ)由A~B知,A与B有相同的特征值,而由|μE一B|=0,可得B的特征

(Ⅱ)

(Ⅰ)求y的概率密度fY(y);
(Ⅱ)求期望ET.
解(Ⅰ)由已知,X1与X2相互独立,故(X1,X2)的概率密度为
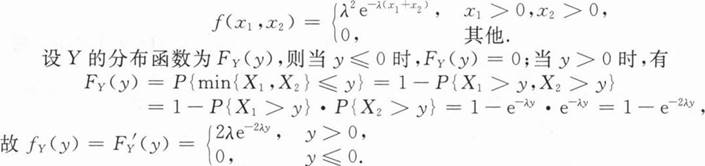
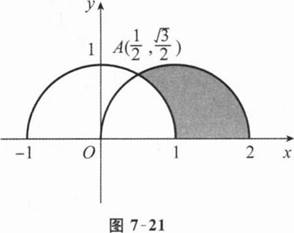
(II)先求T的分布函数与概率密度.