2016年硕士研究生《数学(三)》真题
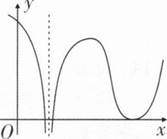
A.函数f(x)有2个极值点,曲线y=f(x)有2个拐点
B.函数f(x)有2个极值点,曲线y=f(x)有3个拐点
C.函数f(x)有3个极值点,曲线y=f(x)有1个拐点
D.函数f(x)有3个极值点,曲线y=f(x)有2个拐点
B
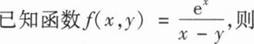 ( ).
( ).A.
B.
C.
D.
D
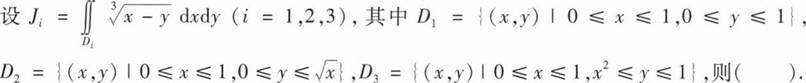
A.J1 B.J3 C.J2 D.J2
B
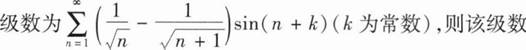 ( ).
( ).A.绝对收敛
B.条件收敛
C.发散
D.收敛性与k有关
A
A.AT与BT相似
B.A-1与B-1相似
C.A+AT与B+BT相似
D.A+A-1与B+B-1相似
C
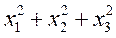 )+2x1x2+2x2x3+2x1x3的正、负惯性指数分别为1,2,则( ).
)+2x1x2+2x2x3+2x1x3的正、负惯性指数分别为1,2,则( ).A.a>1
B.a<-2
C.-2 D.a=1或a=-2
C
A.P( |
| )=1
)=1
B.P(A| )=0
)=0
C.P(A∪B)=1
D.P(B|A)=1
A
A.6
B.8
C.14
D.15
C
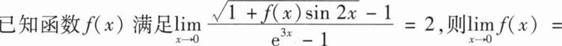 ________.
________.6
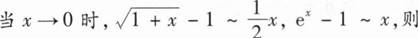
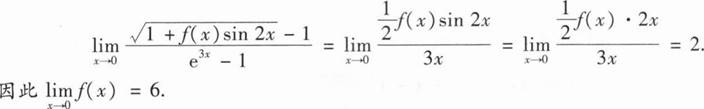
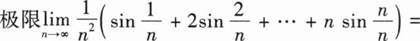 ________.
________.sin1-cos1
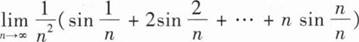
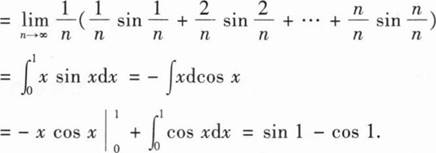
-dx+2dy
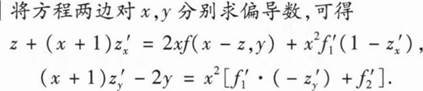
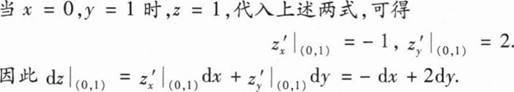
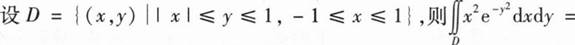 ________.
________.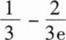
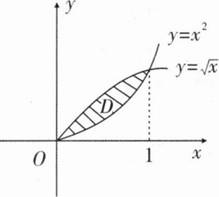
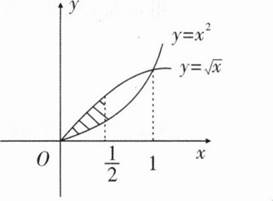
积分区域如右图所示,可知D关于y轴对称,设D1为区域右半部分,则
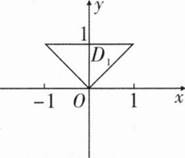
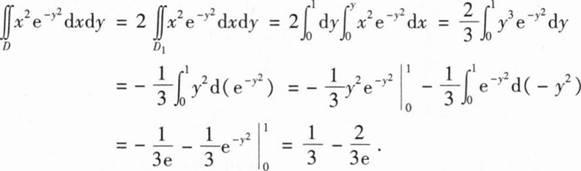
 ________.
________.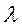 4+
4+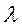 3+2
3+2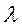 2+3
2+3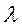 +4
+4本题考查利用行列式的展开求行列式值.

由分析可知:前三次取球中只取到了两种颜色的球,最后一次取的球的颜色不能在前面出现.例如:第四次取到红球,则前三次为两次取白球,一次取黑球;或者一次取白球,两次取黑球,故所求概率为
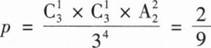
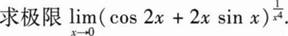
解:
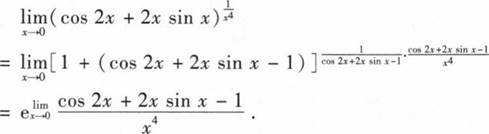


(I)求需求函数的表达式;
(Ⅱ)求p=100万元时的边际收益,并说明其经济意义.

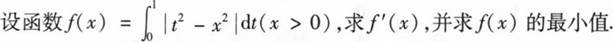
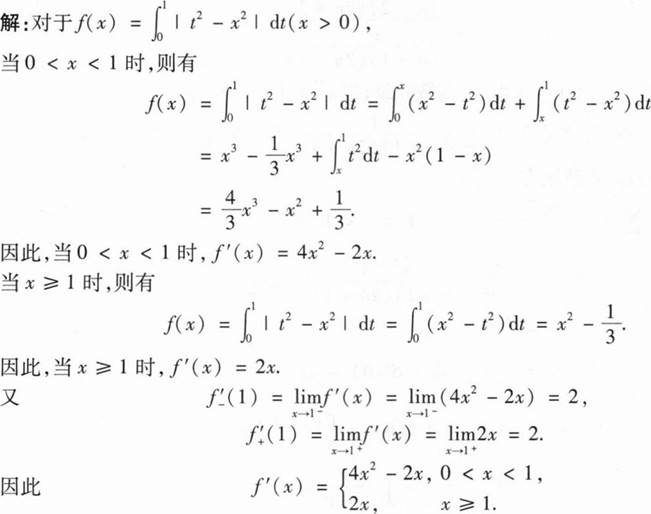

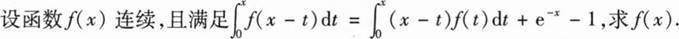

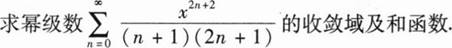

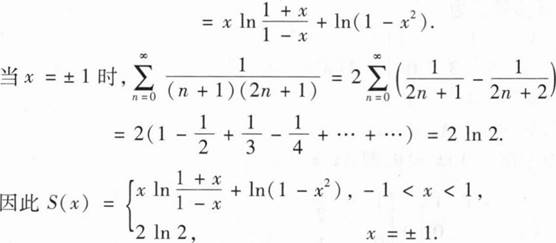
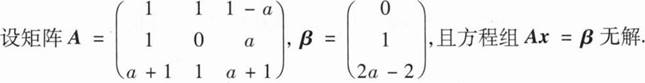
(I)求a的值;
(Ⅱ)求方程组ATAx=ATβ的通解.

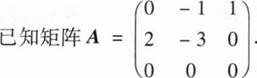
(I)求A99;
(Ⅱ)设三阶矩阵B=(α1,α2,α3)满足B2=BA,记B100=(β1,β2,β3),将β1,β2,β3分别表示为α1,α2,α3的线性组合.


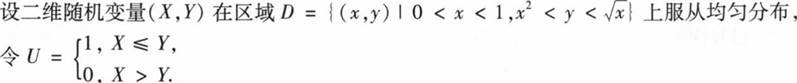
(I)写出(X,Y)的概率密度函数;
(1I)U与X是否相互独立?并说明理由;
(Ⅲ)求Z=U+X的分布函数F(z).
解:(I)区域D的面积
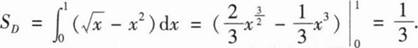

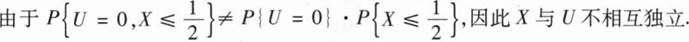
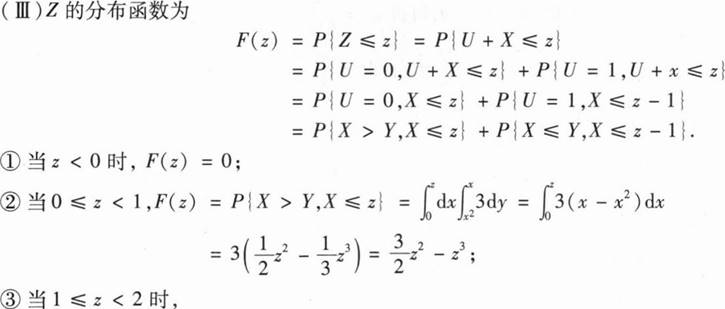
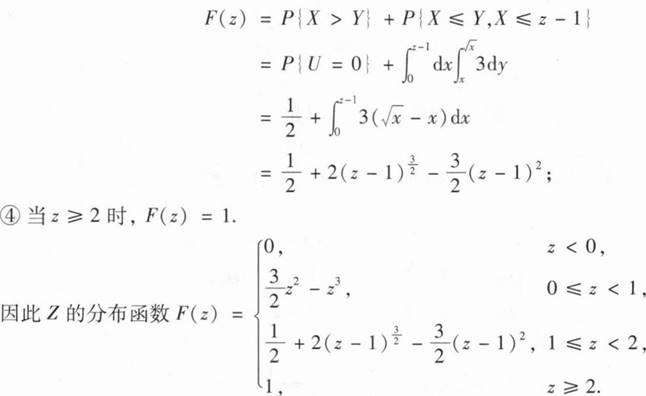
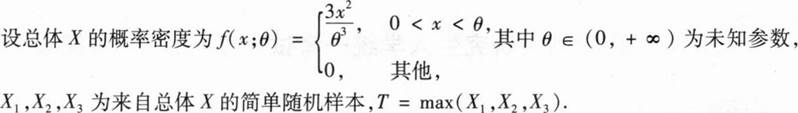
(I)求T的概率密度;
(1I)确定a值,使得E(aT)=θ.

最近更新试卷
Copyright © 奋学网(www.fxuexi.com)All Right Reserved.湘ICP备2021013332号-3