2017年硕士研究生《数学(二)》真题
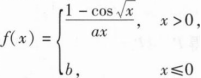 在x=0处连续,则().
在x=0处连续,则().A.ab=
B.ab=-
C.ab=0
D.ab=2
A
A.
B.
C.
D.
B
A.
B.
C.
D.
D
A.Ae2x+e2x(Bcos2x+Csin2x)
B.Axe2x+e2x(Bcos2x+Csin2x)
C.Ae2x+xe2x(Bcos2x+Csin2x)
D.Axe2x+xe2x(Bcos2x+Csin2x)
C
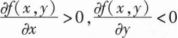 ,则().
,则().A.f(0,0)>f(1,1)
B.f(0,0) C.f(0,1)>f(1,0) D.f(0,1)
D
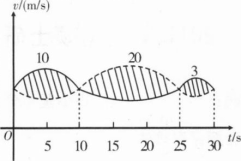
A.t0=10
B.150<20
C.t0=25
D.t0>25
C
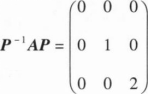 ,则A(α1+α2+α3)=().
,则A(α1+α2+α3)=().A.α1+α2
B.α2+2α3
C.α2+α3
D.α1+2α2
B
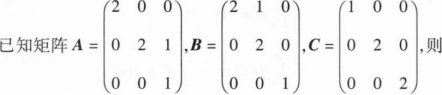
A.A与C相似,B与C相似
B.A与C相似,B与C不相似
C.A与C不相似,B与C相似
D.A与C不相似,B与C不相似
B
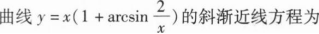 _______.
_______.y=x+2
【解析】
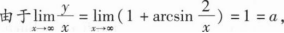
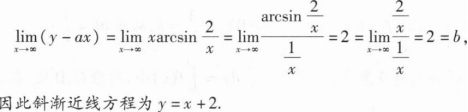
 _______.
_______.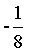
【解析】
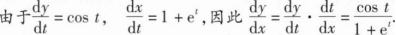
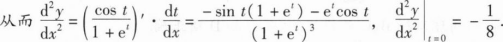
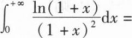 _______.
_______.1【解析】
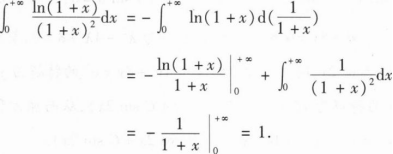
xyey
【解析】
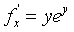 ,
,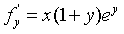 .由于f(x,y)=
.由于f(x,y)=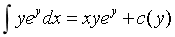 ,因此
,因此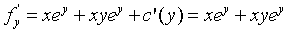 ,则
,则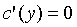 得c(y)=C.又f(0,0)=0,可得C=0,因此f(x,y)=xyey
得c(y)=C.又f(0,0)=0,可得C=0,因此f(x,y)=xyey 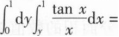 _______.
_______.-lncos1【解析】交换积分次序求解.
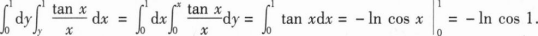
 _______.
_______.-1
【解析】设α=(1,1,2)T,由题设知Aα=λα,故有
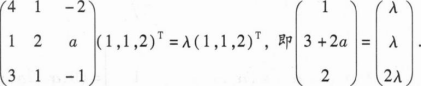
从而可得λ=1,a=-1.

令x-t=u,则t=x-u,dt=-du,从而
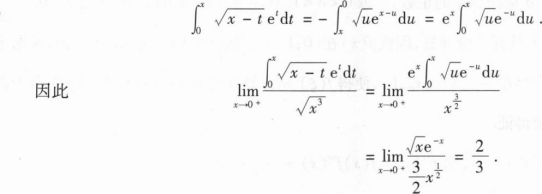
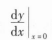 ,
,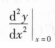 。
。解:由y=f(ex,cosx),可得y(0)=f(1,1),且
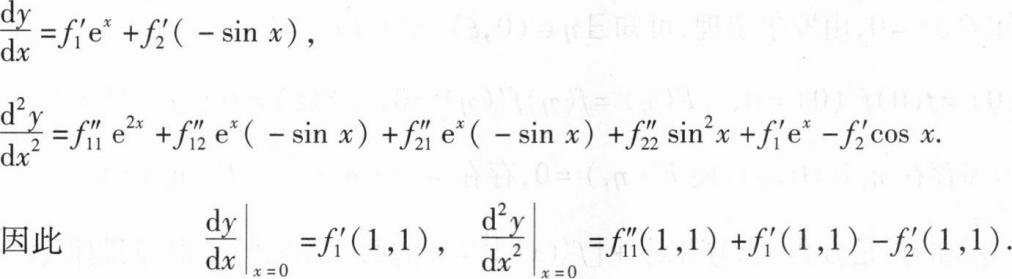
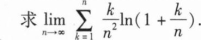
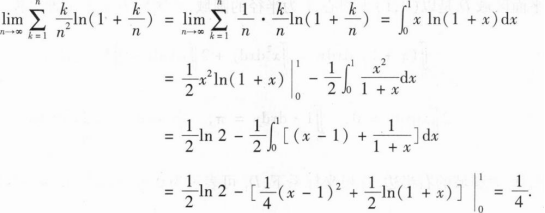
将方程x3+y3—3x+3y-2=0两边关于x分别求一阶、二阶导数可得
3x2+3y2y’-3+3y'=0,①
6x+6y(y’)2+3y2y”+3y”=0.②

将x=1,y=1及y'(1)=0代入②式,可得y”(1)=-1<0.
因此x=1是极大值点,极大值为y(1)=1.
将x=-1,y=0及y’(-1)=0代入②式,可得y”(-1)=2>0.
因此x=-1是极小值点,极小值为y(-1)=0.
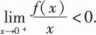 证明:
证明:(I)方程f(x)=0在区间(0,1)内至少存在一个实根;
(Ⅱ)方程f(x)f”(x)+[f’(x)]2=0在区间(0,1)内至少存在两个不同的实根.
证明:(I)
由于
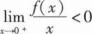 ,根据极限的保号性,可知∃δ>0,对
,根据极限的保号性,可知∃δ>0,对


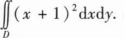
平面区域D是以(0,1)为圆心,1为半径的圆域,且区域D关于y轴对称.

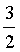 )内的可导函数,且y(1)=0,点P是曲线L:y=y(x)上的任意一点,L在点P处的切线与Y轴相交于点(0,Yp),法线与x轴相交于点(XP,0).若XP=YP,求L上
)内的可导函数,且y(1)=0,点P是曲线L:y=y(x)上的任意一点,L在点P处的切线与Y轴相交于点(0,Yp),法线与x轴相交于点(XP,0).若XP=YP,求L上点的坐标(x,y)满足的方程.

(I)证明:r(A)=2;
(Ⅱ)若β=α1+α2+α3,求方程组Ax=β的通解.

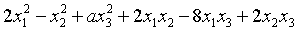 在正交变换x=Qy下的标准形为
在正交变换x=Qy下的标准形为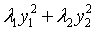 ,求a的值及一个正交矩阵Q.
,求a的值及一个正交矩阵Q.