2017年硕士研究生《数学(一)》真题
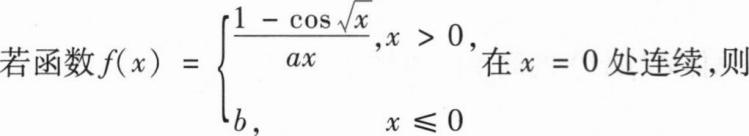
A.ab=
B.ab=-
C.ab=0
D.ab=2
A
A.f(1)>f(-1)
B.f(1) C.|f(1)|>|f(-1)| D.|f(1)|<|f(-1)|
C
A.12
B.6
C.4
D.2
D
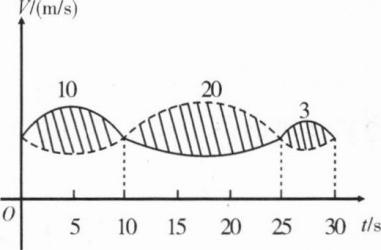
A.t0=10
B.15 C.t0=25 D.t0>25
C
A.E-ααT不可逆
B.E+ααT不可逆
C.E+2ααT不可逆
D.E-2ααT不可逆
A
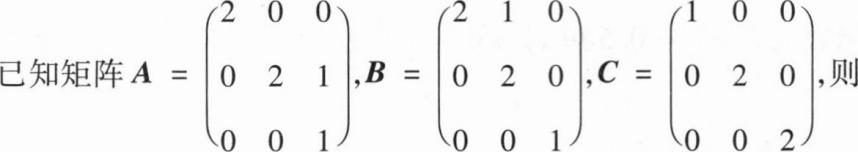
A.A与C相似，B与C相似
B.A与C相似，B与C不相似
C.A与C不相似，B与C相似
D.A与C不相似，B与C不相似
B
)的充分必要条件是（）．
A.P(B|A)>P(B|
)
B.P(B|A)
C.P(
|A)>P(B|
)
D.P(
|A)
A
，则下列结论中不正确的是（）．A.
B.
C.
D.
B
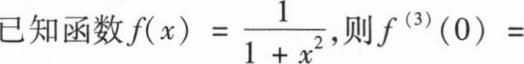
0
【解析】
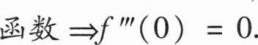
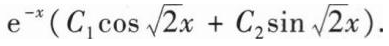
【解析】
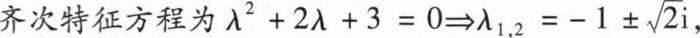
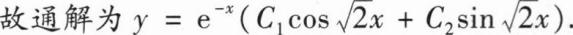
内与路径无关，则a=______.-1
【解析】
______.
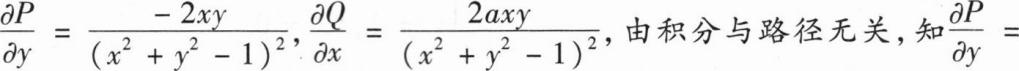
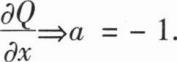
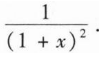
【解析】
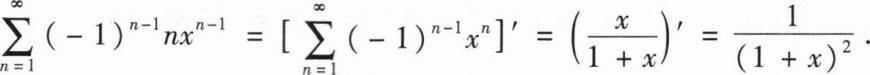
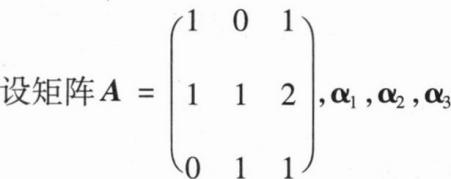为线性无关的三维列向量组，则向量组Aα1，Aα2，Aα3的秩为______.2
【解析】
由α1，α2，α3线性无关可知矩阵(α1，α2，α3)可逆，故r(Aα1，Aα2，Aα3)=r(A(α1，α2，α3))=r(A)，再由r(A)=2得r(Aα1，Aα2，Aα3)=2．
，其中
(x)为标准正态分布函数，则E(X)=______.2
【解析】
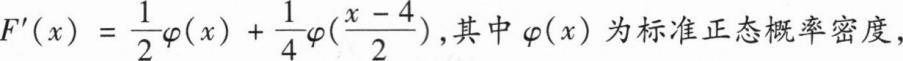
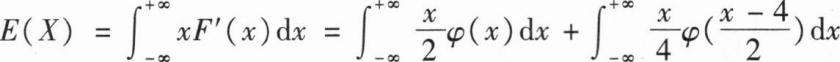
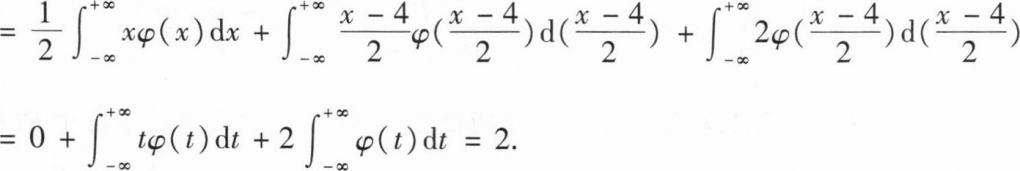
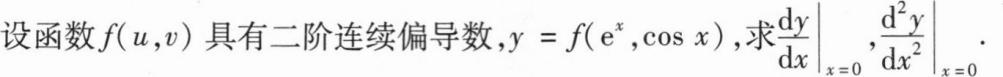
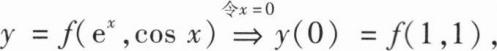
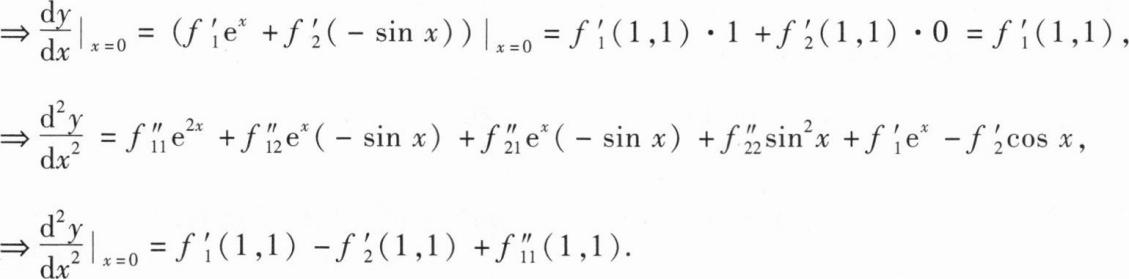
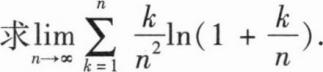
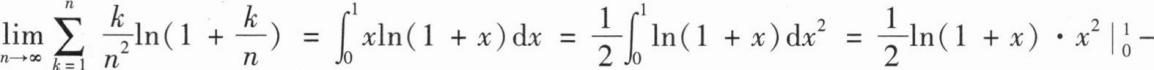
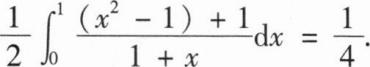
解：两边求导得
(I)方程f(x)=0在区间(0，1)内至少存在一个实根；
(Ⅱ)方程f(x)f”(x)+[f’(x)]2=0在区间(0，1)内至少存在两个不同的实根．
证明：
(I)
又由于f(x)在[δ，1]上连续，由f(δ)<0,f(1)>0，根据零点定理得至少存在一点ξ∈(δ，1)，使f(ξ)=0，即得证．
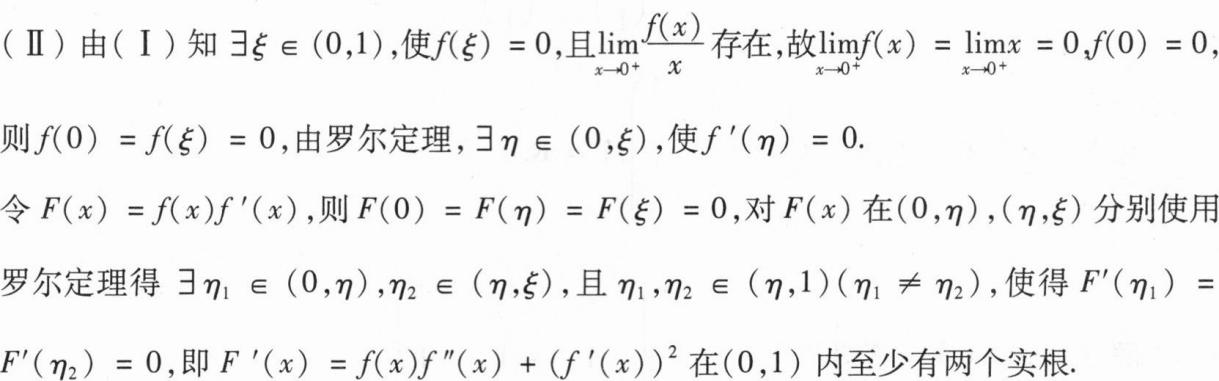
被柱面z2=2x割下的有限部分，其上任一点的密度为u(x，y，z)=9
，记圆锥面与柱面的交线为C．(I)求C在xOy面上的投影曲线的方程；
(Ⅱ)求S的质量M．
(Ⅰ)
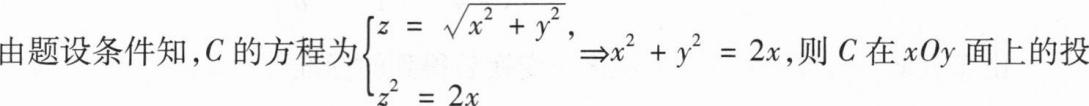
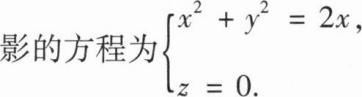
(Ⅱ)
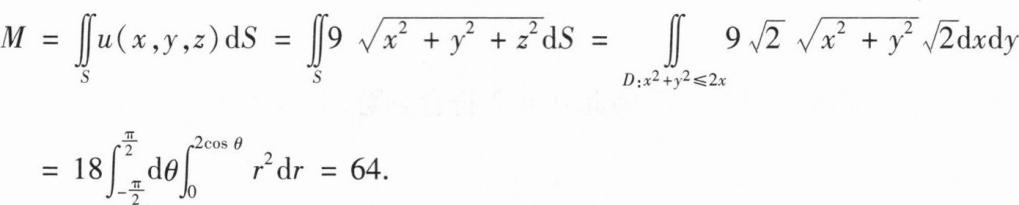
(I)证明：r(A)=2；
(11)如果β=α1+α2+α3，求方程组Ax=β的通解．
解：(I)由α3=α1+2α2可得α1+2α2-α3=0，即α1，α2，α3线性相关，因此，|A|=0，
即A的特征值必有0．
又因为A有三个不同的特征值，则三个特征值中只有1个0，另外两个非0，
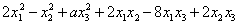在正交变换x=Qy下的标准形为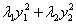
，求a的值及一个正交矩阵Q．
，Y的概率密度为
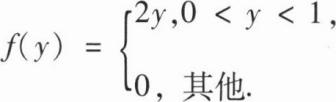
(I)求P{Y≤E(Y)}；
(II)求Z=X+Y的概率密度．
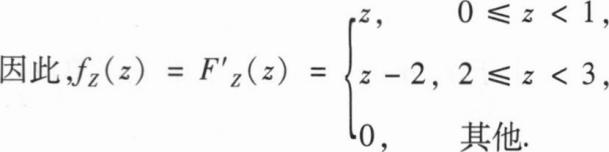
是已知的，设n次测量结果X1，X2，…，Xn相互独立且均服从正态分布N(μ，σ2)，该工程师
记录的是n次测量的绝对误差Zi=|Xi-μ|(i=1，2，…，n)，利用Z1，Z2，…，Zn估计σ．
(I)求Zi的概率密度；
(Ⅱ)利用一阶矩求σ的矩估计量；
(Ⅲ)求σ的最大似然估计量．
