2020年硕士研究生《数学(一)》真题
搜题
1、当x→0+时,下列无穷小量中是最高阶的是( ).
A.
B.
C.
D.
本题答案:
D
D
2、设函数f(x)在区间(-1,1)内有定义,且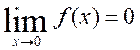 ,则( )
,则( )
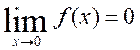 ,则( )
,则( )A.
B.
C.
D.
本题答案:
C
C
3、设函数f(x,y)在点(0,0)处可微f(0,0)=0,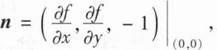 且非零向量d与n垂直,则( ).
且非零向量d与n垂直,则( ).
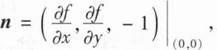 且非零向量d与n垂直,则( ).
且非零向量d与n垂直,则( ).A.
B.
C.
D.
本题答案:
A
A
4、设R为幂级数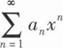 的收敛半径,r是实数,则( ).
的收敛半径,r是实数,则( ).
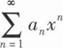 的收敛半径,r是实数,则( ).
的收敛半径,r是实数,则( ).A.
B.
C.
D.
本题答案:
A
A
5、若矩阵A经初等列变换化成B,则( ).
A.存在矩阵P,使得PA=B
B.存在矩阵P,使得BP=A
C.存在矩阵P,使得PB=A
D.方程组Ax=0与Bx=0同解
本题答案:
B
B
6、已知直线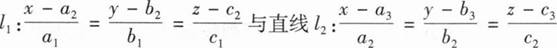 相交于一点,法向量
相交于一点,法向量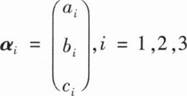 ,则( ).
,则( ).
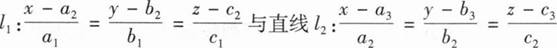 相交于一点,法向量
相交于一点,法向量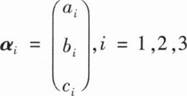 ,则( ).
,则( ).A. 可由a2,a3线性表示
可由a2,a3线性表示
B. 可由a1,a3线性表示
可由a1,a3线性表示
C. 可由a1,a2线性表示
可由a1,a2线性表示
D. ,a2,a3线性无关
,a2,a3线性无关
本题答案:
C
C
7、设A,B,C为三个随机事件,P(A)=P(B)=P(C)=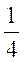 ,P(AB)=O,P(AC)=P(BC)=1,则A,B,C中恰有一个事件发生的概率为( ).
,P(AB)=O,P(AC)=P(BC)=1,则A,B,C中恰有一个事件发生的概率为( ).
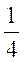 ,P(AB)=O,P(AC)=P(BC)=1,则A,B,C中恰有一个事件发生的概率为( ).
,P(AB)=O,P(AC)=P(BC)=1,则A,B,C中恰有一个事件发生的概率为( ).A.
B.
C.
D.
本题答案:
D
D
8、设X1,X2,…,Xn为来自总体X的简单随机样本,其中P{X=0}=P{X=1}=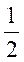 ,
,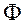 (x)
(x)
表示标准正态分布函数,则利用中心极限定理可得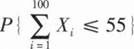 的近似值为( ).
的近似值为( ).
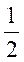 ,
,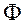 (x)
(x)表示标准正态分布函数,则利用中心极限定理可得
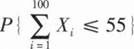 的近似值为( ).
的近似值为( ).A.1- (1)
(1)
B. (1)
(1)
C.1- (0.2)
(0.2)
D. (0.2)
(0.2)
本题答案:
B
B
9、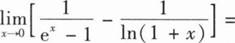
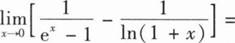
本题答案:
-1
【解析】

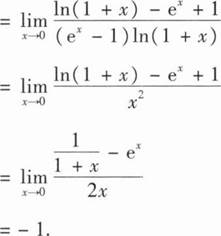
-1
【解析】

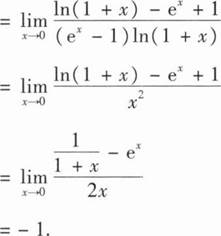
10、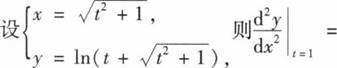
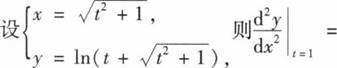
本题答案:
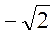
【解析】

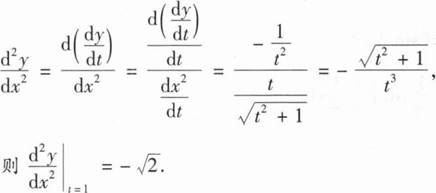
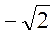
【解析】

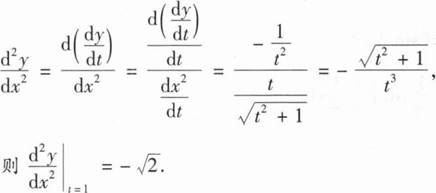
11、若函数f(x)满足f”(x)+af’(x)+f(x)=0(a>0),且f(0)=m,f'(0)=n,则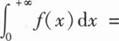
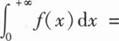
本题答案:
n+am
【解析】
特征方程为λ2+aλ+1=0(a>0),设特征根为λ1,λ2,则λ1+λ2=-a,
λ1λ2=1,特征辛艮λ1<0,λ2<0.

n+am
【解析】
特征方程为λ2+aλ+1=0(a>0),设特征根为λ1,λ2,则λ1+λ2=-a,
λ1λ2=1,特征辛艮λ1<0,λ2<0.

12、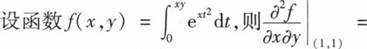
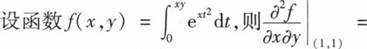
本题答案:
4e
【解析】
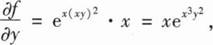
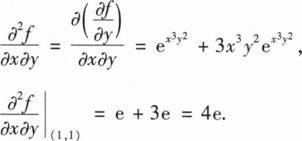
4e
【解析】
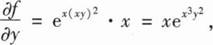
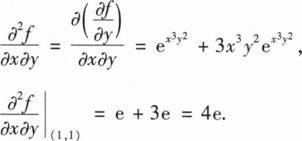
13、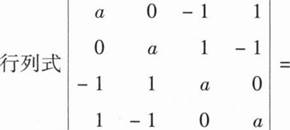
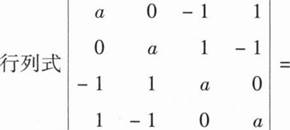
本题答案:
a4-4a2
【解析】
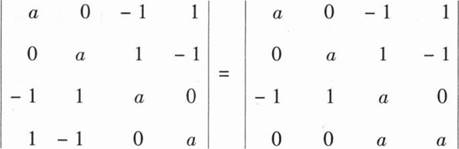
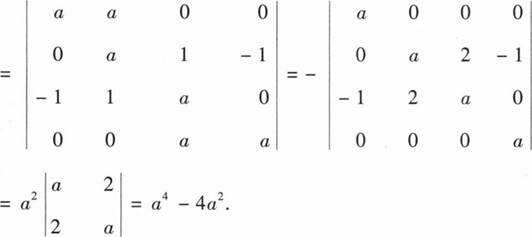
a4-4a2
【解析】
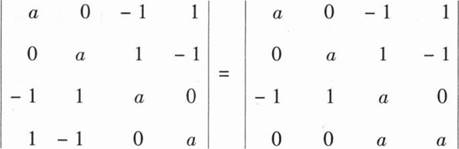
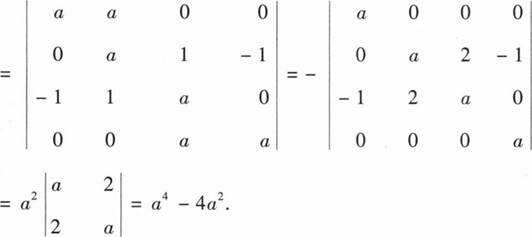
14、设X服从区间(-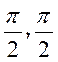 )上的均匀分布,Y=sinX,则Cov(X,Y)=——.
)上的均匀分布,Y=sinX,则Cov(X,Y)=——.
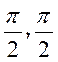 )上的均匀分布,Y=sinX,则Cov(X,Y)=——.
)上的均匀分布,Y=sinX,则Cov(X,Y)=——.
本题答案:

【解析】

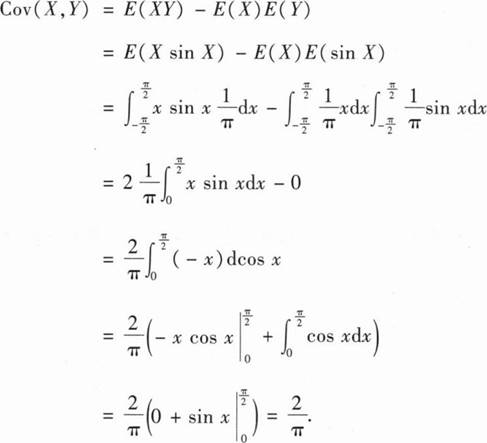

【解析】

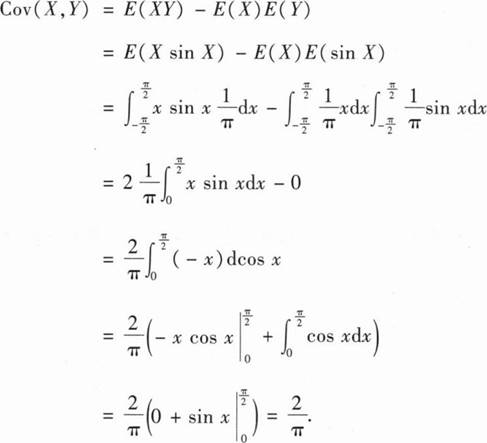
15、求函数f(x,y)=x3+8y3-xy的极值.
本题答案:
求一阶导数可得

求一阶导数可得

16、计算曲线积分
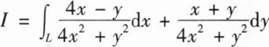 ,其中L是x2+y2=2,方向为逆时针方向.
,其中L是x2+y2=2,方向为逆时针方向.
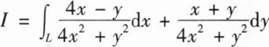 ,其中L是x2+y2=2,方向为逆时针方向.
,其中L是x2+y2=2,方向为逆时针方向.
本题答案:
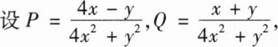

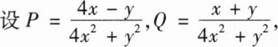

17、设数列{an}满足a1=1,(n+1)an+1=(n+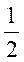 )an,证明:当|x|<1时,幂级数
)an,证明:当|x|<1时,幂级数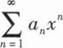 收敛,并求其和函数.
收敛,并求其和函数.
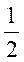 )an,证明:当|x|<1时,幂级数
)an,证明:当|x|<1时,幂级数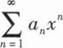 收敛,并求其和函数.
收敛,并求其和函数.
本题答案:
由(n+1)an+1=(n+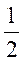 )an,a1=1知an>0,
)an,a1=1知an>0,

由(n+1)an+1=(n+
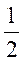 )an,a1=1知an>0,
)an,a1=1知an>0,
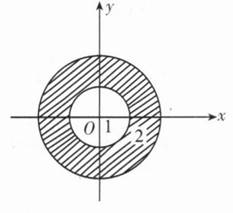
18、设∑为曲面z=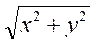 (1≤x2+y2≤4)的下侧,f(x)是连续函数,计算I=
(1≤x2+y2≤4)的下侧,f(x)是连续函数,计算I=
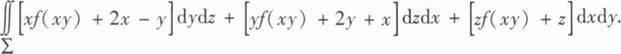
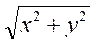 (1≤x2+y2≤4)的下侧,f(x)是连续函数,计算I=
(1≤x2+y2≤4)的下侧,f(x)是连续函数,计算I=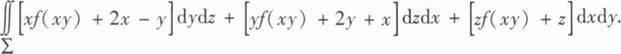
本题答案:
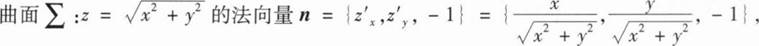
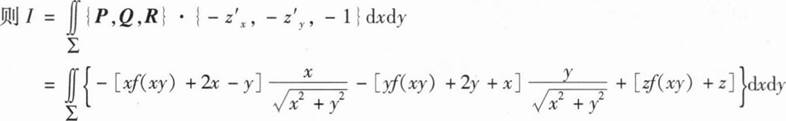
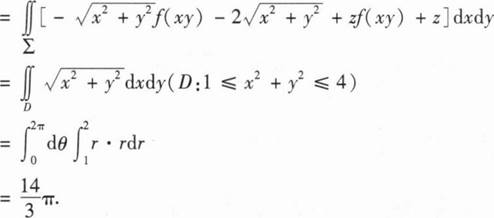
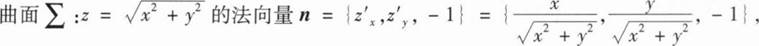
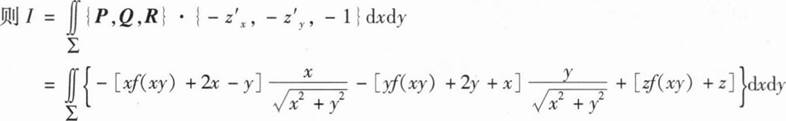
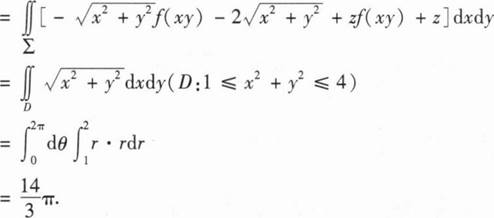

19、设函数f(x)在区间[0,2]上具有连续导数f(0)=f(2)=0,M=max{|f(x)|},x∈[0,2],
证明:(Ⅰ)存在ξ∈(0,2),使得|f'(ξ)|≥M;
(Ⅱ)若对任意的x∈(0,2),|f’(x)|≤M,则M=0.
证明:(Ⅰ)存在ξ∈(0,2),使得|f'(ξ)|≥M;
(Ⅱ)若对任意的x∈(0,2),|f’(x)|≤M,则M=0.
本题答案:
(Ⅰ)由M=max{|f(x)|},x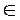 [0,2]知存在c∈(0,2),使|f(c)|=M.若
[0,2]知存在c∈(0,2),使|f(c)|=M.若
c∈(0,1],由拉格朗日中值定理得至少存在一点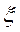 ∈(0,c),使
∈(0,c),使

(Ⅱ)若M>0,则c≠0,2.
由f(0)=f(2)=0及罗尔定理知存在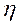 ∈(0,2),使f’(
∈(0,2),使f’(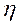 )=0.
)=0.
当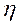 /∈(0,c]时,
/∈(0,c]时,
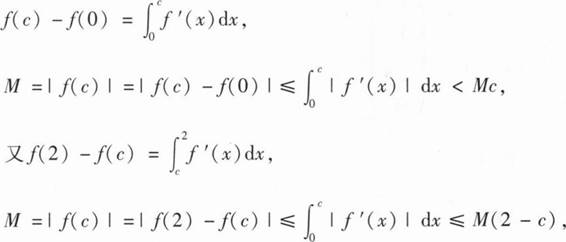
于是2M故M=0.
(Ⅰ)由M=max{|f(x)|},x
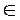 [0,2]知存在c∈(0,2),使|f(c)|=M.若
[0,2]知存在c∈(0,2),使|f(c)|=M.若c∈(0,1],由拉格朗日中值定理得至少存在一点
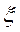 ∈(0,c),使
∈(0,c),使
(Ⅱ)若M>0,则c≠0,2.
由f(0)=f(2)=0及罗尔定理知存在
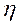 ∈(0,2),使f’(
∈(0,2),使f’(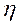 )=0.
)=0.当
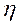 /∈(0,c]时,
/∈(0,c]时,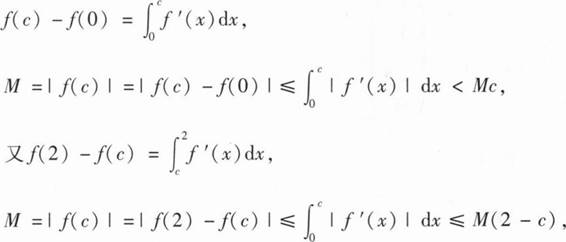
于是2M
20、设二次型f(x1,x2)=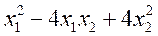 经正交变换
经正交变换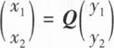 化为二次型g(y1,y2)=
化为二次型g(y1,y2)=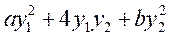 ,其中a≥b.
,其中a≥b.
(Ⅰ)求a,b的值;
(Ⅱ)求正交矩阵Q.
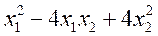 经正交变换
经正交变换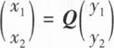 化为二次型g(y1,y2)=
化为二次型g(y1,y2)=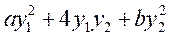 ,其中a≥b.
,其中a≥b.(Ⅰ)求a,b的值;
(Ⅱ)求正交矩阵Q.
本题答案:
(I)
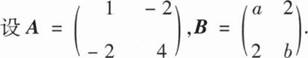
由题意可知QTAQ=Q-1AQ=B,
∴A相似于B,
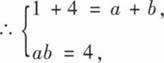
a≥b.
∴a=4.b=1.
(Ⅱ)

∴A的特征值为0,5.
当λ=0时,解(OE—A)x=0得基础解为
当λ=5时,解(5E—A)x=0得基础解为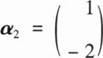
又B的特征值也为0,5,
当λ=0时,解(0E-B)x=0得
当λ=5时,解(5E-B)x=0得
对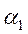 ,
,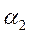 单位化,得
单位化,得

(I)
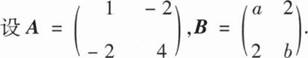
由题意可知QTAQ=Q-1AQ=B,
∴A相似于B,
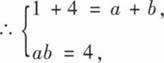
a≥b.
∴a=4.b=1.
(Ⅱ)

∴A的特征值为0,5.
当λ=0时,解(OE—A)x=0得基础解为

当λ=5时,解(5E—A)x=0得基础解为
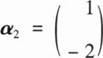
又B的特征值也为0,5,
当λ=0时,解(0E-B)x=0得

当λ=5时,解(5E-B)x=0得

对
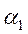 ,
,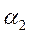 单位化,得
单位化,得
21、设A为二阶矩阵,P=(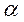 ,A
,A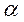 ),其中
),其中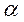 是非零向量且不是A的特征向量.
是非零向量且不是A的特征向量.
(I)证明P为可逆矩阵;
(Ⅱ)若A2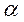 +A
+A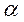 -6
-6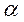 =0,求P-1AP,并判断A是否相似于对角矩阵.
=0,求P-1AP,并判断A是否相似于对角矩阵.
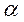 ,A
,A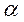 ),其中
),其中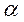 是非零向量且不是A的特征向量.
是非零向量且不是A的特征向量.(I)证明P为可逆矩阵;
(Ⅱ)若A2
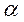 +A
+A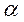 -6
-6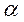 =0,求P-1AP,并判断A是否相似于对角矩阵.
=0,求P-1AP,并判断A是否相似于对角矩阵.
本题答案:
(I)因为 ≠0且
≠0且 不是A的特征向量,所以A
不是A的特征向量,所以A ≠
≠
 ,
,
故 与A
与A 线性无关,
线性无关,
则r( ,A
,A )=2,
)=2,
则P可逆.
(11)解法一
因为A2 +A
+A -6
-6 =0,即A2
=0,即A2 =-A
=-A +6
+6 ,
,
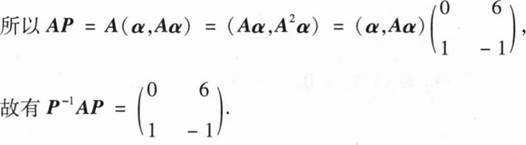

解得 =-3,2,
=-3,2,
所以A的特征值为-3,2.于是A可相似对角化.
解法二
P-1AP同解法一.
由A2 +A
+A -6
-6 =0,
=0,
得(A2+A-6E) =0,
=0,
即(A+3E)(A-2E) =0,
=0,
由 ≠0得(A2+A-6E)x=0有非零解,
≠0得(A2+A-6E)x=0有非零解,
故|(A+3E)(A-2E)|=0,
得|A+3E|=0或|A-2E|=0.
若|A+3E|≠0,则(A一2E) =0,故A
=0,故A =2
=2 与题意矛盾,
与题意矛盾,
故|A+3E|=0,同理可得|A-2E|=0.
于是A的特征值为-3,2,
A有2个不同特征值,故A可相似对角化.
(I)因为
 ≠0且
≠0且 不是A的特征向量,所以A
不是A的特征向量,所以A ≠
≠
 ,
,故
 与A
与A 线性无关,
线性无关,则r(
 ,A
,A )=2,
)=2,则P可逆.
(11)解法一
因为A2
 +A
+A -6
-6 =0,即A2
=0,即A2 =-A
=-A +6
+6 ,
,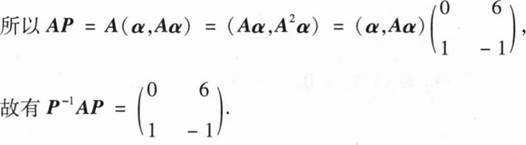

解得
 =-3,2,
=-3,2,所以A的特征值为-3,2.于是A可相似对角化.
解法二
P-1AP同解法一.
由A2
 +A
+A -6
-6 =0,
=0,得(A2+A-6E)
 =0,
=0,即(A+3E)(A-2E)
 =0,
=0,由
 ≠0得(A2+A-6E)x=0有非零解,
≠0得(A2+A-6E)x=0有非零解,故|(A+3E)(A-2E)|=0,
得|A+3E|=0或|A-2E|=0.
若|A+3E|≠0,则(A一2E)
 =0,故A
=0,故A =2
=2 与题意矛盾,
与题意矛盾,故|A+3E|=0,同理可得|A-2E|=0.
于是A的特征值为-3,2,
A有2个不同特征值,故A可相似对角化.
22、设随机变量X1,X2,X3相互独立,其中X1与X2均服从标准正态分布,X3的概率分布为P{X3=0}=P{X3=1}=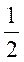 ,Y=X3X1+(1-X3)X2.
,Y=X3X1+(1-X3)X2.
(Ⅰ)求二维随机变量(X1,Y)的分布函数,结果用标准正态分布函数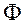 (x)表示;
(x)表示;
(Ⅱ)证明随机变量Y服从标准正态分布.
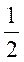 ,Y=X3X1+(1-X3)X2.
,Y=X3X1+(1-X3)X2.(Ⅰ)求二维随机变量(X1,Y)的分布函数,结果用标准正态分布函数
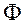 (x)表示;
(x)表示;(Ⅱ)证明随机变量Y服从标准正态分布.
本题答案:
(I)F(x,y)=P{x,≤x,Y≤y}

若x>y,则 P{X1≤x,X1≤y|X3=1}=
P{X1≤x,X1≤y|X3=1}= P{X1≤y}=
P{X1≤y}=
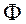 (y),
(y),

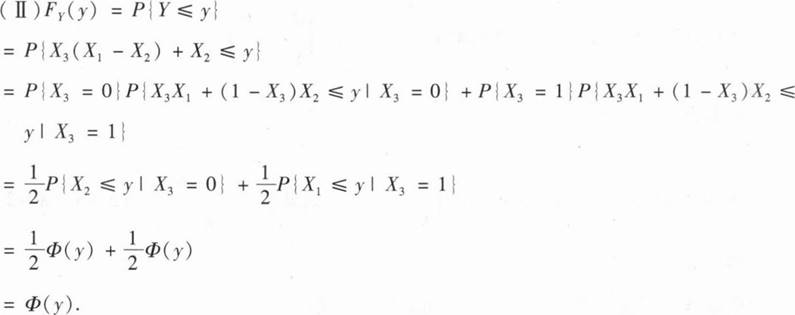
(I)F(x,y)=P{x,≤x,Y≤y}

若x>y,则
 P{X1≤x,X1≤y|X3=1}=
P{X1≤x,X1≤y|X3=1}= P{X1≤y}=
P{X1≤y}=
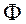 (y),
(y),
23、设某种元件的使用寿命T的分布函数为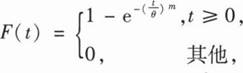 其中0,m为参数且大于零.
其中0,m为参数且大于零.
(Ⅰ)求概率P{T>t}与P{T>s+t|T>s},其中s>0,t>0;
(Ⅱ)任取n个这种元件做寿命试验,测得它们的寿命分别为t1,t2,…,tn,若m已知,求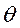 的最大似然估计值
的最大似然估计值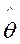 .
.
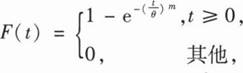 其中0,m为参数且大于零.
其中0,m为参数且大于零.(Ⅰ)求概率P{T>t}与P{T>s+t|T>s},其中s>0,t>0;
(Ⅱ)任取n个这种元件做寿命试验,测得它们的寿命分别为t1,t2,…,tn,若m已知,求
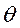 的最大似然估计值
的最大似然估计值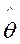 .
.
本题答案: