2019年硕士研究生《数学(三)》真题
搜题
1、当x→0时，x-tanx与xk是同阶无穷小，则k=( )．
A.1
B.2
C.3
D.4
本题答案：
C
C
2、已知方程x5-5x+k=0有3个不同的实根，则k的取值范围是( )．
A.(-∞，-4)
B.(4，+∞)
C.[-4，4]
D.(-4，4)
本题答案：
D
D
3、已知微分方程y”+ay'+by=cex的通解为y=(C1+C2x)e-x+ex，则a，b，c依次为( )．
A.1，0，1
B.1，0，2
C.2，1，3
D.2，1，4
本题答案：
D
D
4、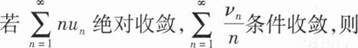
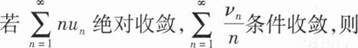
A.
B.
C.
D.
本题答案：
B
B
5、设A是四阶矩阵，A*是A的伴随矩阵，若线性方程Ax=0的基础解系中只有2个向量，则A*的秩是( )．
A.0
B.1
C.2
D.3
本题答案：
A
A
6、设A是三阶实对称矩阵，E是三阶单位矩阵，若A2+A=2E，且|A|=4，则二次xTAx的规范形为( )．
A.
B.
C.
D.
本题答案：
C
C
7、设A，B为随机事件，则P(A)=P(B)的充分必要条件是( )．
A.P(A∪B)=P(A)+P(B)
B.P(AB)=P(A)P(B)
C.P(A
)=P(B
)
D.P(AB)=P(
)
本题答案：
C
C
8、设随机变量X和Y相互独立，且都服从正态分布N(μ，σ2)，则P{|X-Y|<1}( )．
A.与μ无关，而与σ2有关
B.与μ有关，而与σ2无关
C.与μ，σ2都有关
D.与μ，σ2都无关
本题答案：
A
A
9、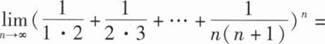
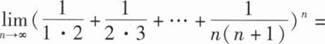
本题答案：
【解析】
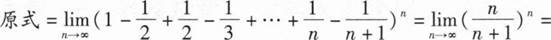
【解析】
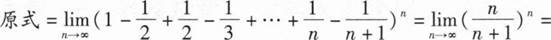
10、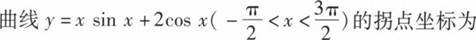
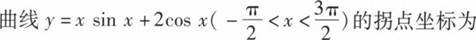
本题答案：
(π，-2)
【解析】
y’=sinx+xcosx-2sinx=xcosx-sinx．
y”=cosx-xsinx-cosx=-xsinx．
令y”=0，得x=0，x=π
又在x=0的左右两侧，y”<0，故(0，2)不是拐点．
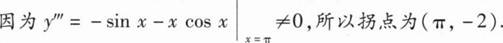
(π，-2)
【解析】
y’=sinx+xcosx-2sinx=xcosx-sinx．
y”=cosx-xsinx-cosx=-xsinx．
令y”=0，得x=0，x=π
又在x=0的左右两侧，y”<0，故(0，2)不是拐点．
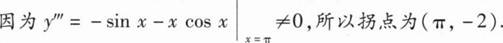
11、
本题答案：
【解析】
【解析】
12、A、B两商品的价格分别表示为PA、PB，设A商品的需求函数QA=500-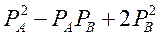
，则当PA=10，PB=20时，商品A的需求量对自身价格需求弹性
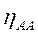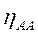(>0)=________．
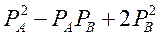，则当PA=10，PB=20时，商品A的需求量对自身价格需求弹性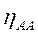(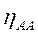>0)=________．
本题答案：
0．4
【解析】
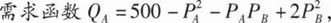
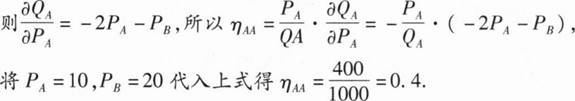
0．4
【解析】
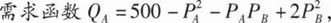
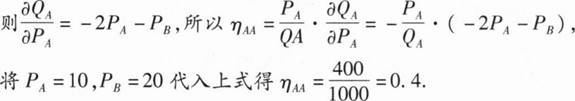
13、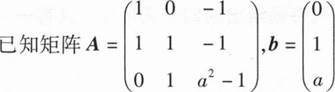
，若线性方程组Ax=b有无穷多解，则a=
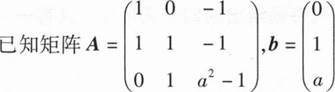，若线性方程组Ax=b有无穷多解，则a=
本题答案：
1
【解析】
当a=1时，r(A)=r(A)=2<3，方程组Ax=b有无穷多解，故a=1．
1
【解析】
当a=1时，r(A)=r(A)=2<3，方程组Ax=b有无穷多解，故a=1．
14、设连续型随机变量x的概率密度为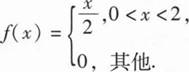
F(X)为x的分布函数，E(X)为X的数学期望，则P{F(X)>E(X)-1}=________．
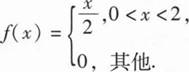F(X)为x的分布函数，E(X)为X的数学期望，则P{F(X)>E(X)-1}=________．
本题答案：
【解析】
解法一
【解析】
解法一
15、
本题答案：
解：
解：
16、设函数f(u，v)具有二阶连续偏导数，函数g(x，y)=xy-f(x+y，x-y)，求
本题答案：
解：
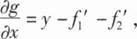
解：
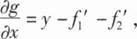
17、设函数y(x)是微分方程
满足条件y(1)=
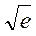的特解．
(I)求y(x)；
(II)设平面区域D={(x，y)|1≤x≤2，0≤y≤y(x)}，求D绕x轴旋转一周所得旋转体的体积．
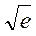满足条件y(1)=的特解．(I)求y(x)；
(II)设平面区域D={(x，y)|1≤x≤2，0≤y≤y(x)}，求D绕x轴旋转一周所得旋转体的体积．
本题答案：
解：(I)
解：(I)
18、求曲线Y=e-xsinx(x≥0)与x轴之间围成的图形的面积．
本题答案：
解：
解：
19、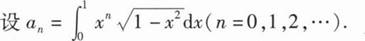
(I)证明：数列{an}单调递减，且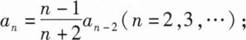
(Ⅱ)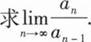
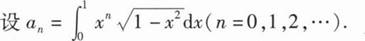
(I)证明：数列{an}单调递减，且
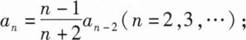
(Ⅱ)
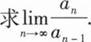
本题答案：
解：(I)
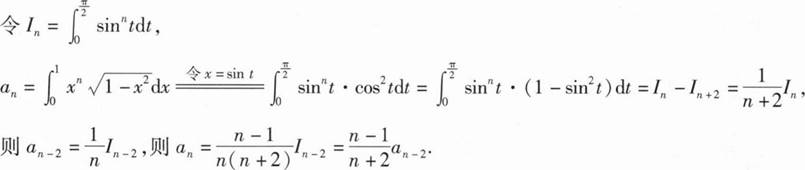
解：(I)
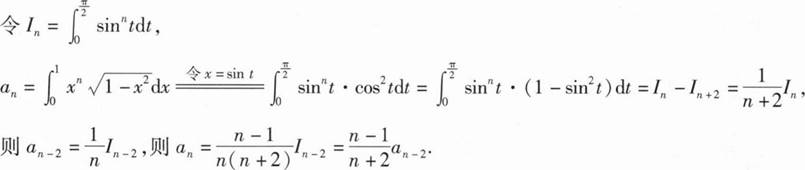
20、
本题答案：
解：
解：
21、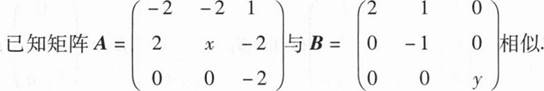
(I)求x，y；
(Ⅱ)求可逆矩阵P使得P-1AP=B．
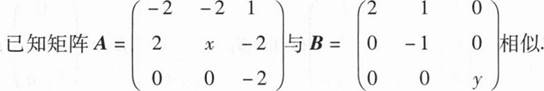
(I)求x，y；
(Ⅱ)求可逆矩阵P使得P-1AP=B．
本题答案：
解：(I)
解：(I)
22、设随机变量X与Y相互独立，X服从参数为1的指数分布，Y的概率分布为P{Y=-1}=P，P{Y=1}=1-p，(0(I)求Z的概率密度；
(Ⅱ)p为何值时，X与Z不相关?
(III)X与Z是否相互独立?
(Ⅱ)p为何值时，X与Z不相关?
(III)X与Z是否相互独立?
本题答案：
解：
解：
23、设总体X的概率密度为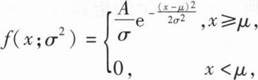
其中μ是已知参数，σ>0是未知参
数，A是常数，X1，X2，…，Xn是来自总体X的简单随机样本．
(I)求A；
(Ⅱ)求σ2的最大似然估计量．
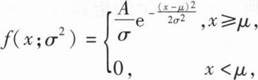其中μ是已知参数，σ>0是未知参数，A是常数，X1，X2，…，Xn是来自总体X的简单随机样本．
(I)求A；
(Ⅱ)求σ2的最大似然估计量．
本题答案：
解：
解：